Türev
Giriş
İçindekiler
Bu yazıda matematikte çok önemli bir konu olan türevi, temeline inerek anlaşılabilir şekilde izah etmeye çalıştım.
Türev konusu için trigonometri, limit, denklemler ve eğrileri gibi temel bilgilere sahip olunması gerekir. Bununla birlikte iyi bir altyapınız olmasa da türev hakkında elle tutulur bilgiye sahip olacaksınız. Hiç bir şey olmazsa türev nedir? diyenlere eğimdir! dersiniz olur biter; Bu da bir şeydir.
Türev, herhangi bir eğrinin, herhangi bir noktasından geçen teğetinin, eğimini hesaplama işlemidir. Yani türev ile eğim aynı şeydir. Dersin ilerleyen kısımlarında konu daha iyi anlaşılacaktır.
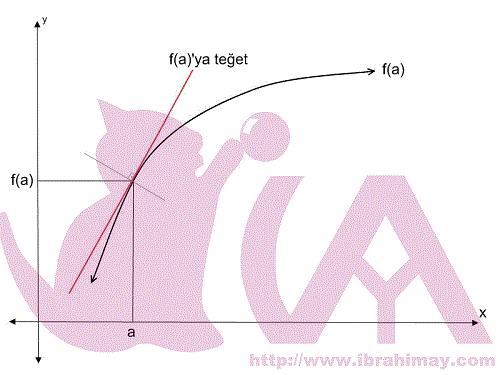
Aşağıda herhangi bir f(x) denkleminin çizdiği eğri görülmektedir.
Bu denklemin x=a iken türevinin sorulması ile bu eğriye a noktasından teğet geçen doğrunun eğiminin sorulması aynı şeydir.
f(a)’ya teğet geçen doğrunun eğimi için, teğet ile x ekseni arasındaki açı demek yanlış değildir. Aşağıda görüldüğü gibi hipotenüsü teğet, dik kenarları x ve y eksenleri olan bir dik üçgen çizilebilmektedir.
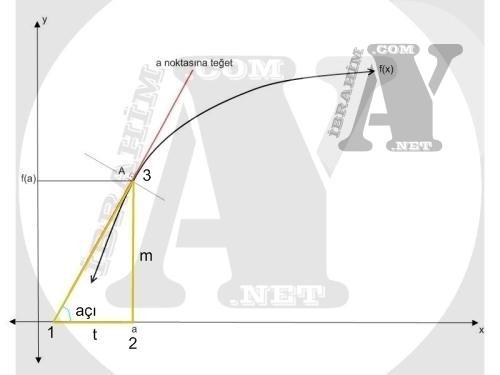
Bir dik üçgende eğim; açının gördüğü kenarın, komşu kenara bölünmesi ile bulunur. Bulunan bu değerin ters tanjantı açıyı verir. Yani
eğim e= m/t tir. Veya açı = tan-1(e). Buradan tan(açı)=e=m/t olduğunu çıkarabiliriz.
Yukarıda A noktasından geçen teğetin eğimini bu hali ile bulamıyoruz. m uzunluğu (2-3) f(a)’ya eşit olduğu için biliyoruz ancak teğetin uzatılarak x eksenini kestiği nokta ile A arası olan 3-1 mesafesini ve yine aynı nokta ile a arası olan (1-2 mesafesi) t’yi bilmiyoruz. Bu üçgenin iki kenarını bilsek üçüncüyü bulurduk ancak sadece f(a) mesafesini, diğer bir ifade ile sadece y’yi biliyoruz.
İşte türev, bu bilinmezliği limit yardımı ile çözerek eğimi bulmamıza yarayan mükemmel bir yöntemdir.