Yarılama (İkiye Bölme veya Bisection) Yöntemi

Tahmin İle Çözüme Başlamak

Tahmin İle Çözüme Başlamak

Örnek 1/2

f(x) = 5x+4

y=0 için x=?

Konu anlatımı için böyle basit bir örnekle başlamayı uygun buldum.

Çözüm:

x₁ için y>0 x₂ için y<0 yapan iki değer seçelim.

(Not: x₁ için y<0 x₂ için y>0’da olabilir) x₁=1 dersem

f(x₁) =5x₁ + 4 = 5*1 + 4 = 9 y>0 uygundur.

x₂= -1 dersem f(x₂) = 5x₂ + 4 = 5*-1 + 4 = -1

y<0 uygundur. x₁ veya x₂ değerlerinizden biri f(x)’i sıfır yapıyorsa zaten çözümü atmasyon yöntemi ile elde etmişsiniz demektir.

x₃= (x₁+x₂)/2=(1-1)/2=0/2=0 x₃=0

f(x₃) = 5x₃ + 4 = 5*0 + 4 = 4

Adım	x1	x2	x3	f(x1)	f(x2)	f(x3)
1	1	-1	0	9	-1	4

Adım 2’ye geçmek için baktığımızda y=0 değeri f(x₂) ile f(x₃) arasında kaldı. Dikkat edin, kıyaslamaları x₁-x₃ ile x₂-x₃ arsında yapıyoruz. Başlangıç değerlerimizi (x₁ ve x₂‘yi) zaten y=0’ı ortalayacak şekilde biz seçtik, x₁-x₂ arasında değerlendirme yapmanın anlamı yok. y=0 değeri f(x₂) ile f(x₃) arasında kaldığına göre x₂ değişmeyecektir. x₁‘i değiştirip yerine x₃‘ü yazacağız.

Kıyaslamayı birde şu şekilde yapalım:

x₁ için f(x₁)*f(x₃)<0 ise x₁;x₃

f(x₁)*f(x₃)=36 olduğundan x₁ yerine x₃ yazılır. Bu durumda x₂ değişmeyecek demektir ama biz yine de kontrol edelim.

x₂ için f(x₂)*f(x₃)<0 ise x₂;x₃

-4<0 olduğu için x₂ değişmez. İlla çarpma yapmanıza gerek yok. f(x)’lerin işaretlerinden, neticenin pozitif mi? negatif mi? olacağı bellidir.

Benzer işaretli sayıların çarpımları pozitif (-)*(-)=(+)_____(+)*(+)=(+)

Farklı işaretli sayıların çarpımları negatiftir (-)*(+)=(-)_____(+)*(-)=(-)

x₃= (x₁+x₂)/2=(0-1)/2=-1/2=-0,5

Adım	x1	x2	x3	f(x1)	f(x2)	f(x3)
1	1	-1	0	9	-1	4
2	0	-1	-0,5

f(x₁) = 5x₁ + 4 = 5*0 + 4 = 4

f(x₂) = 5x₂ + 4 = 5*-1 + 4 = -1

f(x₃) = 5x₃ + 4 = 5*-0,5 + 4 = 1,5

Adım	x1	x2	x3	f(x1)	f(x2)	f(x3)
1	1	-1	0	9	-1	4
2	0	-1	-0,5	4	-1	1,5

Görüldüğü gibi başlangıç aralığımız daralarak 0’a yaklaşıyor.

Adım 3 ve ileriside yukarıdaki adımların tekrarıdır. Neticeyi 1/100 hassasiyette bırakacağız.

Adım	x1	x2	x3	f(x1)	f(x2)	f(x3)
1	1	-1	0	9	-1	4
2	0	-1	-0,5	4	-1	1,5
3	-0,5	-1	-0,75	1,5	-1	0,25
4	-0,75	-1	-0,875	0,25	-1	-0,375
5	-0,75	-0,875	-0,8125	0,25	-0,375	-0,0625
6	-0,75	-0,8125	-0,78125	0,25	-0,0625	0,0938
7	-0,78125	-0,8125	-0,796875	0,0938	-0,0625	0,0156
8	-0,796875	-0,8125	-0,804688	0,0156	-0,0625	-0,0234
9	-0,796875	-0,804688	-0,800781	0,0156	-0,0234	-0,0039

9. adımda f(x₃) = -0,0039 çıktı. .Neticede x= -0,800781 değerini bulmuş oluruz.

1/100 hassasiyet ile x= -0,800781 için y=0 diyebiliriz.

Bu basit örneğimiz de x’i net olarak çözebileceğimiz için kıyaslayalım.

5x+4=0

x= -4/5 = -0,8’dir

-0,8-0,800781

Eğer adımları daha da ilerletirseniz net olarak -0,8 değerine kesinlikle ulaşacağınıza şüpheniz olmasın.

Daha önce de belirttiğim gibi konunun izahı için basit bir denklemle konu anlatımında bulundum.

Örnek 2/2

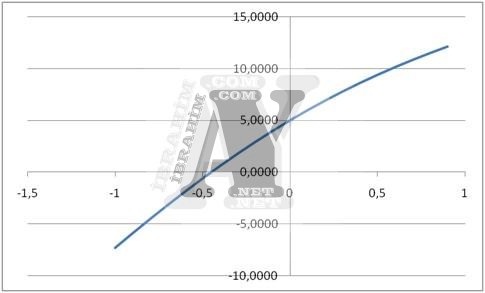
f(x)=10x + 5cos(x) = 0 için 1/1000 hassasiyetle x=?

f(x₁) = -1 için

f(x₁) = 10*(1) + 5cos(1) = -7,2985

f(x₂) = 2 için

f(x₂) = 10*(2) + 5cos(2) = 17,9193

Adım	x1	x2	x3	f(x1)	f(x2)	f(x3)
1	-1,000000	2,000000	0,500000	-7,2985	17,9193	9,3879
2	-1,000000	0,500000	-0,250000	-7,2985	9,3879	2,3446
3	-1,000000	-0,250000	-0,625000	-7,2985	2,3446	-2,1952
4	-0,625000	-0,250000	-0,437500	-2,1952	2,3446	0,1541
5	-0,625000	-0,437500	-0,531250	-2,1952	0,1541	-1,0016
6	-0,531250	-0,437500	-0,484375	-1,0016	0,1541	-0,4189
7	-0,484375	-0,437500	-0,460938	-0,4189	0,1541	-0,1312
8	-0,460938	-0,437500	-0,449219	-0,1312	0,1541	0,0117
9	-0,460938	-0,449219	/sub -0,455078	-0,1312	0,0117	-0,0596
10	-0,455078	-0,449219	-0,452148	-0,0596	0,0117	-0,0239
11	-0,452148	-0,449219	-0,450684	-0,0239	0,0117	-0,0061
12	-0,450684	-0,449219	-0,449951	-0,0061	0,0117	0,0028
13	-0,450684	-0,449951	-0,450317	-0,0061	0,0028	-0,0016
14	-0,450317	-0,449951	-0,450134	-0,0016	0,0028	0,0006

f(x)=10x + 5cos(x) = 0 için x = -0,450134 (1/1000 hassasiyet ile)