Yarılama (İkiye Bölme veya Bisection) Yöntemi

Tepe Noktalarını Bularak Çözüme Başlamak

Tepe Noktalarını Bularak Çözüme Başlamak

f(x)=3x²+ 7x -12

y=0 için x=?

Denklemimiz 2. derecedendir ve çözüm kümesinde 2 eleman vardır.

Yarıya bölme yöntemi ile çözümde tahmini değerlerimizden bir tanesini

x_aiçin x_a1=x_t

x_biçin x_b1=x_t olarak alabiliriz.

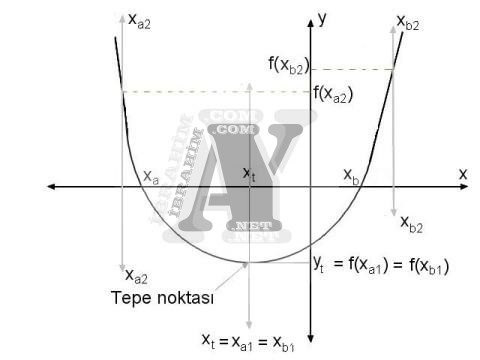
x_t denklem eğrisinin tepe noktaları olan y_t ‘leri veren değerlerdir. 2. dereceden denklemde (derece-1) 1 tepe noktası vardır.

Bir denklemin türevinin çözüm kümesindeki değerler, denklemin tepe noktalarını veren değerlerdir.

2. dereceden denklemimizin türevi 1. dereceden olacaktır ve 1. dereceden denklemlerin çözüm kümesinde 1 eleman vardır. Dolayısıyla 1 tepe noktası vardır.

f(x)=3x²+ 7x -12

f(x)^‘=6x + 7

6x + 7=0 için

x= -7/6

Denklemimizde ki eğrinin tepe noktası x_t= -7/6’da dır.

y_t=3x_t²+ 7x_t -12=3(-7/6)²+ 7(-7/6) -12

y_t = – 16,0833

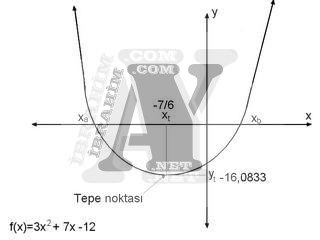
x_aiçin x_a1=x_t

x_biçin x_b1=x_t

f(x_a1)=f(x_t)=y_t

f(x_b1)=f(x_t)=y_t

dedikten sonra x_a2 ve x_b2‘yi şöyle tespit edebiliriz:

f(x_a2) ve f(x_b2)’nin işareti f(x_t)’nin işaretinin tersi netice verecek şekilde tahmin edilmelidir. Böylece y=0 için x değeri tahmini değerlerimiz olan (x_a1x_a2) ve (x_b1x_b2) arasında kalır. Yani

(f(x_a1)*f(x_a2)<0

(f(x_b1)*f(x_b2)<0olmalıdır.

x_a için çözüm

x_a1= -7/6’yı tepe noktası olarak belirlemiştik.

x_a2 = -3 diyelim (Tepe noktasının solundan seçtim. Bu durumda x_b2 ‘yi seçerken sağından seçmeliyim)

(f(x_a1)*f(x_a2)<0

f(x_a2)=3x_a2²+ 7x_a2 -12 = 3(-3)² + 7(-3) – 12 = 27-21-12= -6

(f(x_a1)*f(x_a2)<0 koşulunu -16,0833*-6 sağlamadığı için x_a2 = -3 için çözüme gidemeyiz.

x_a2 = -8 diyelim

f(x_a2)=3x_a2²+ 7x_a2 -12 = 3(-8)² + 7(-8) – 12 = 192-56-12= 124

(f(x_a1)*f(x_a2)<0 koşulu için -16,0833*124<0 olduğu için x_a2 = -8 ile çözüme gidebiliriz.

Adım	xa1	xa2	xa3	f(xa1)	f(xa2)	f(xa3)
1	-7/6	-8,000000	-4,583333	-16,0833	124,0000	18,9375
2	-7/6	-4,583333	-2,875000	-16,0833	18,9375	-7,3281
3	-2,875000	-4,583333	-3,729167	-7,3281	18,9375	3,6159
4	-2,875000	-3,729167	-3,302083	-7,3281	3,6159	-2,4033
5	-3,302083	-3,729167	-3,515625	-2,4033	3,6159	0,4695
6	-3,302083	-3,515625	-3,408854	-2,4033	0,4695	-1,0011
7	-3,408854	-3,515625	-3,462240	-1,0011	0,4695	-0,2744
8	-3,462240	-3,515625	-3,488932	-0,2744	0,4695	0,0954
9	-3,462240	-3,488932	-3,475586	-0,2744	0,0954	-0,0900
10	-3,475586	-3,488932	-3,482259	-0,0900	0,0954	0,0026
11	-3,475586	-3,482259	-3,478923	-0,0900	0,0026	-0,0438
12	-3,478923	-3,482259	-3,480591	-0,0438	0,0026	-0,0206
13	-3,480591	-3,482259	-3,481425	-0,0206	0,0026	-0,0090
14	-3,481425	-3,482259	-3,481842	-0,0090	0,0026	-0,0032
15	-3,481842	-3,482259	-3,482051	-0,0032	0,0026	-0,0003

15. adımda 1/1000 hassasiyet için x_a= -3,482051’dir.

x_b için çözüm

x_b1= -7/6’yı tepe noktası olarak belirlemiştik.

x_b2 = 1 diyelim (x_a2 ‘yi tepe noktasının solundan seçmiştim. Bu durumda x_b2 ‘yi seçerken tepe noktasının sağından seçmeliyim)

(f(x_b1)*f(x_b2)<0

f(x_b2)=3x_b2²+ 7x_b2 -12 = 3(1)² + 7(1) – 12 = 3+7-12= -2

(f(x_b1)*f(x_b2)<0 koşulunu -16,0833*-2 sağlamadığı için x_b2 = 1 için çözüme gidemeyiz.

x_b2 = 3 diyelim

f(x_b2)=3x_b2²+ 7x_b2 -12 = 3(3)² + 7(3) – 12 = 27+21-12= 36

(f(x_b1)*f(x_b2)<0 koşulu için -16,0833*36<0 olduğu için x_b2 = 3 ile çözüme gidebiliriz.

Adım	xb1	xb2	xb3	f(xb1)	f(xb2)	f(xb3)
1	-7/6	3,000000	0,916667	-16,0833	36,0000	-3,0625
2	0,916667	3,000000	1,958333	-3,0625	36,0000	13,2135
3	0,916667	1,958333	1,437500	-3,0625	13,2135	4,2617
4	0,916667	1,437500	1,177083	-3,0625	4,2617	0,3962
5	0,916667	1,177083	1,046875	-3,0625	0,3962	-1,3840
6	1,046875	1,177083	1,111979	-1,3840	0,3962	-0,5067
7	1,111979	1,177083	1,144531	-0,5067	0,3962	-0,0584
8	1,144531	1,177083	1,160807	-0,0584	0,3962	0,1681
9	1,144531	1,160807	1,152669	-0,0584	0,1681	0,0546
10	1,144531	1,152669	1,148600	-0,0584	0,0546	-0,0020
11	1,148600	1,152669	1,150635	-0,0020	0,0546	0,0263
12	1,148600	1,150635	1,149618	-0,0020	0,0263	0,0122
13	1,148600	1,149618	1,149109	-0,0020	0,0122	0,0051
14	1,148600	1,149109	1,148855	-0,0020	0,0051	0,0016
15	1,148600	1,148855	1,148727	-0,0020	0,0016	-0,0002

15. adımda 1/1000 hassasiyet için x_b= 1,148727’dur.

y=0 için
x₁= -3,482051
x₂= 1,148727

ile çözersek x₁= -3,482073 x₂= 1,148740

-3,482073 -3,482051

1,148740 1,148727

Daha ileriki adımlarda daha yüksek hassasiyet ile netice bulunur. Burada uzatmanın anlamı yok “,